Skip to content

Pauli Charges (or Vertex Behaviour)

As you add and stack stabilisers in Entwine, the vertices change color to provide immediate visual feedback about the local operator product acting on each qubit. This makes it easy to see where stabilisers overlap, commute, or conflict.

Vertex Colors

Each vertex reflects the type of stabilisers acting on it:

  • Yellow → Vertex belongs to a Z stabiliser (orange).
  • Green → Vertex belongs to an X stabiliser (blue).
  • Black → The net product of Paulis is the identity at this vertex.
  • Magenta → An imbalance occurs: the vertex hosts overlapping anticommuting operators (X and Z, or equivalently Y).

How it Works

  1. When a stabiliser is placed, each vertex inside it inherits the color of that stabiliser’s Pauli operator.
  2. If a vertex is shared by multiple stabilisers, the product of Pauli operators determines its resulting state:
    • Commuting operators (e.g., Z with Z, or X with X) cancel to the identity → vertex turns black.
    • Anticommuting operators (e.g., X and Z) cannot cancel and instead indicate a conflict → vertex turns magenta.

Example Workflow

Let's look again at the creation of a logical block for the rotated surface code:

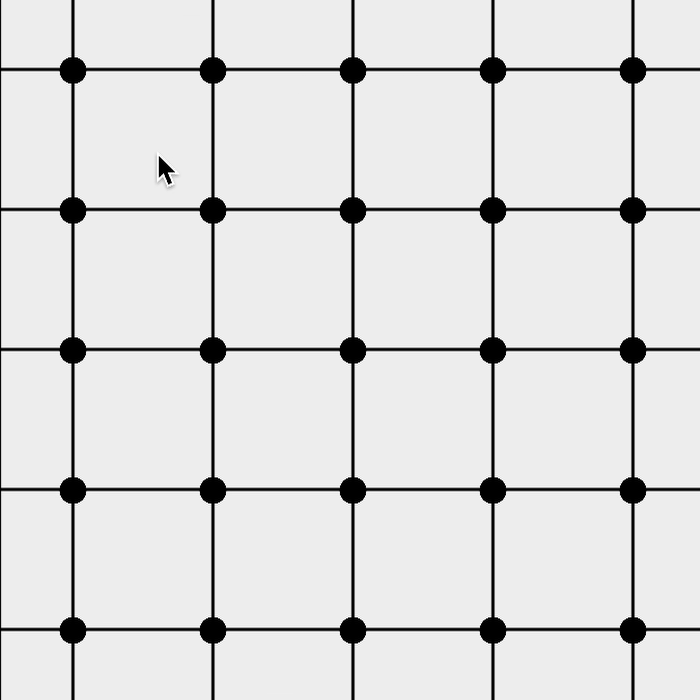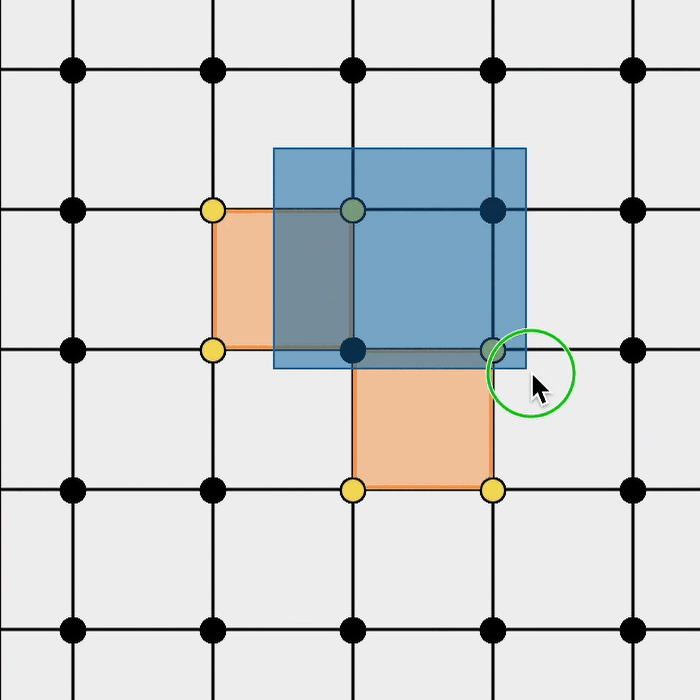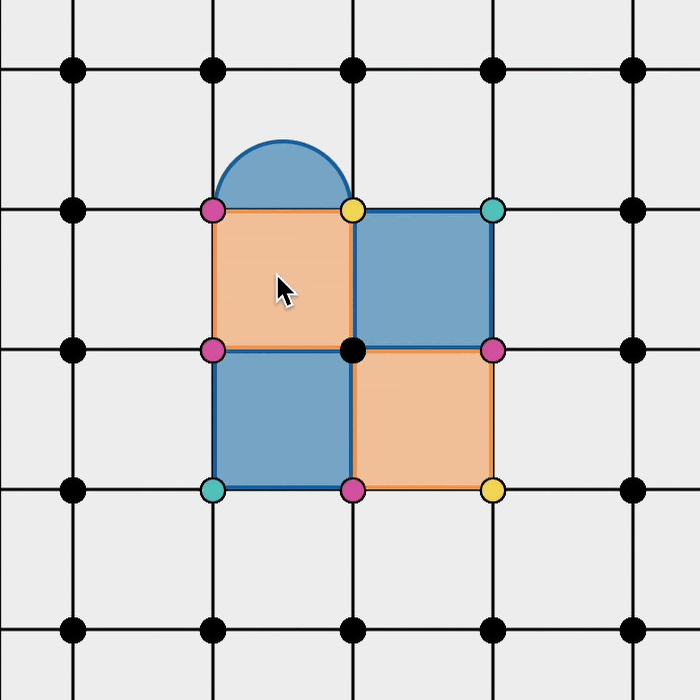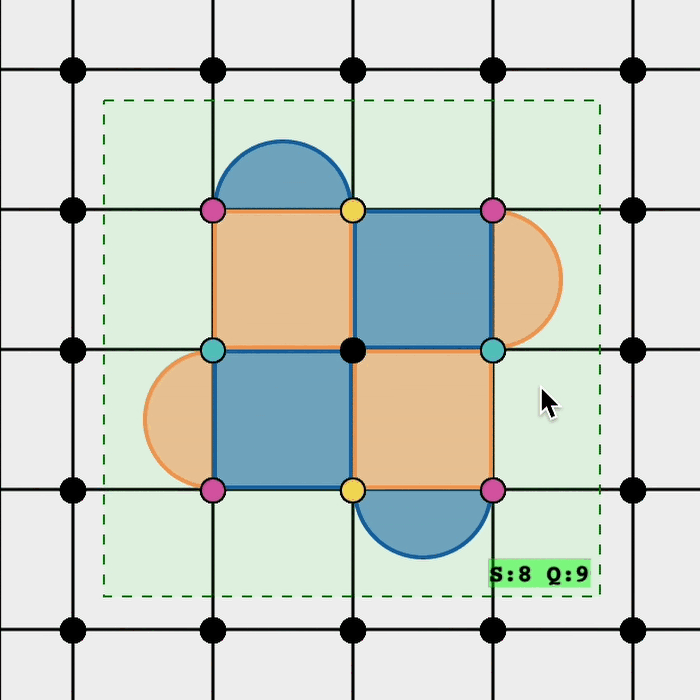
Creating a logical block

  • Adding a Z stabiliser highlights its vertices in yellow.
  • Adding an X stabiliser highlights its vertices in green.
  • Where Z and X stabilisers overlap:
    • If they cancel → vertex becomes black.
    • If they conflict (anticommutation) → vertex becomes magenta.

Why This Matters

Color feedback on vertices helps you:

  • Quickly identify stabiliser overlaps.
  • Debug unbalanced or invalid constructions.
  • Confirm that your patch maintains proper commutation rules between stabilisers.

By combining stabiliser coloring with vertex feedback, Entwine provides a powerful visual language for building and validating surface code structures.