AuxCNOT

In this tutorial, we will learn how to perform a logical CNOT using lattice surgery.

This will show you how to:

• Perform Grow, Shrink, Merge, and Split operations
• Understand how Loom deals internally with these operations
• Perform conditional logical operations
• Validate our result using Stim

---

Overview

In previous tutorials, we learned how to create a QEC code and run a logical experiment. In particular, we used the AuxCNOT operation to create a GHZ state.
In this tutorial, we will dissect the AuxCNOT operation and see how it is built from lattice surgery primitives such as Grow, Shrink, Merge, and Split.
Along the way, we will explore how these operations work and how they transform blocks.
We will also see how to combine these primitives into composite lattice-surgery routines that implement nontrivial logical operations.

At a high level, the AuxCNOT involves the following steps:

1. Grow the control block
2. Split the control block into new control and auxiliary blocks
3. Merge the auxiliary block with the target block into a merged target block
4. Apply ConditionalLogicalZ to the blocks, conditioned on the joint measurement obtained from Merge
5. Shrink the merged target block back to its original size

---

The AuxCNOT operation

We will build our own logical CNOT operation for the rotated surface code.
Remember that you can directly call the final operation as from loom_rotated_surface_code.operations import AuxCNOT.

Step 0: Create the Blocks

We begin by creating two rotated-surface-code Blocks of distance d.

Pay attention to the relative placement of the two blocks.
This is important for the Grow and Merge operations. In particular, we must preserve the alternating stabilizer pattern and ensure that the Split happens at the correct position.
We can do this by shifting the target block by d + 1 cells away from the control block (in both directions).

In the AuxCNOT operation, this placement check is handled for you.

from loom.eka import Lattice
from loom_rotated_surface_code.code_factory import RotatedSurfaceCode


d = 3

lattice = Lattice.square_2d((2 * d + 2, 2 * d + 2))

control_qubit = RotatedSurfaceCode.create(
    dx=d,
    dz=d,
    position=(0, 0),
    lattice=lattice,
    unique_label="control",

)

target_qubit = RotatedSurfaceCode.create(
    dx=d,
    dz=d,
    position=(d + 1, d + 1),
    lattice=lattice,
    unique_label="target",
)

blocks = [control_qubit, target_qubit]

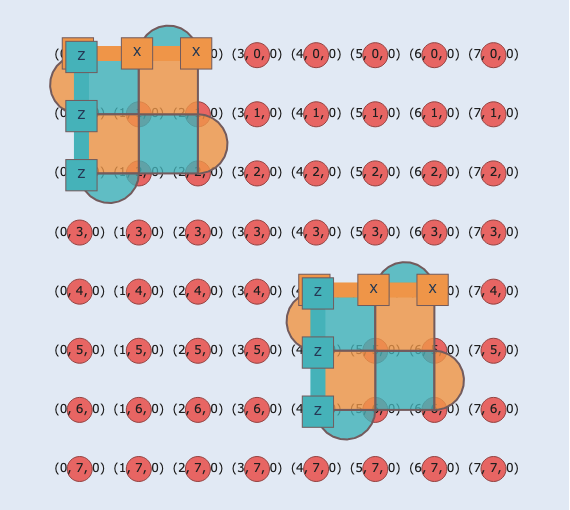
Here you can see what the complete AuxCNOT operation for this particular configuration would look like.
Let us go through it step-by-step.

from loom.eka.utilities import Direction
from loom.eka.operations.code_operation import ConditionalLogicalZ
from loom_rotated_surface_code.code_factory import RotatedSurfaceCode
from loom.eka.operations import (
    ResetAllDataQubits,
    MeasureBlockSyndromes,
    MeasureLogicalZ,
    MeasureLogicalX,
    LogicalMeasurement,
    Grow,
    Split,
    Merge,
    Shrink
)

blocks = (control_qubit, target_qubit)

auxcnot_operations = (
    ( # Grow control
        Grow("control", direction="RIGHT", length=d+1),
    ),
    ( # Measure syndromes
        MeasureBlockSyndromes("control", n_cycles=d),
        MeasureBlockSyndromes("target", n_cycles=d),
    ),
    ( # Split
        Split("control", ("control_new", "aux"),
                    orientation="VERTICAL", split_position=d),
    ),
    ( # Measure syndromes
        MeasureBlockSyndromes("control_new", n_cycles=1),
        MeasureBlockSyndromes("aux", n_cycles=1),
        MeasureBlockSyndromes("target", n_cycles=1),
    ),
    ( # Merge
        Merge(("aux", "target"), "merged_target"),
        MeasureBlockSyndromes("control_new", n_cycles=1),
    ),
    ( # Measure syndromes
        MeasureBlockSyndromes("control_new", n_cycles=d-1),
        MeasureBlockSyndromes("merged_target", n_cycles=d-1),
    ),
    ( # Conditional logical Z (control)
       ConditionalLogicalZ(
           "control_new",
           condition=LogicalMeasurement(("target", "aux"), "XX"),
        ),
    ),
    ( # Conditional logical Z (target)
       ConditionalLogicalZ(
           "merged_target",
           condition=LogicalMeasurement(("target", "aux"), "XX"),
    ),
    ),
    ( # Shrink target
        Shrink("merged_target", direction="TOP", length=d+1),
    ),
)

Step 1: Grow control

First, we grow the control block.
In this tutorial, we grow to the right, which lengthens the logical X operator while leaving the logical Z unchanged.
We grow the control block by d + 1 units so that it aligns with the target block.

After growing, we perform d cycles of error correction.

Note: We could have chosen to grow downward instead, which would lengthen the logical Z operator. It is important to track this choice carefully, because it determines the directions of the subsequent Split and affects the form of the logical correction after merging.

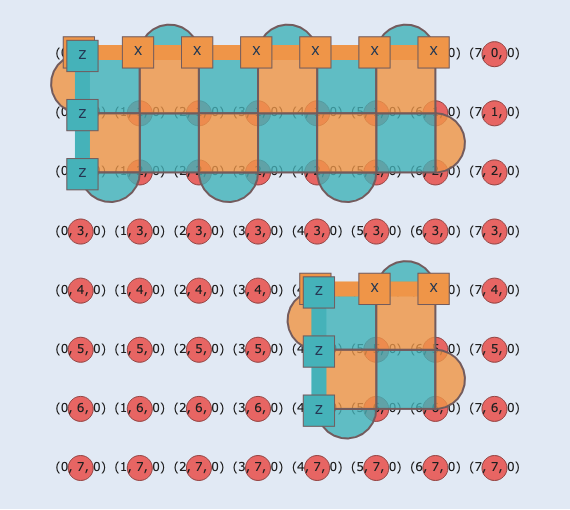
Step 2: Split control

We split the grown control block into control_new and aux, thereby creating the auxiliary qubit used in the CNOT.
The split direction is orthogonal to the direction in which we just grew.
To obtain two blocks of distance d, we split the expanded block at position d.

As a result of the Split, we obtain two new Blocks and a measurement outcome on the split line.
In this case, the logical \(X_\mathrm{control}\) operator is split into \(X_\mathrm{aux}\) and \(X_\mathrm{control\_new}\).
The relationship between the old and new logical operators is \(X_\mathrm{control} = X_\mathrm{aux} \cdot X_\mathrm{control\_new} \cdot x_\mathrm{meas}\), where \(x_\mathrm{meas}\) is the outcome of measuring the operator qubits along the split. We want this transformation to be deterministic, so \(x_\mathrm{meas}\) must be tracked.
In Loom, we ensure determinism by absorbing the measured-qubit outcome into the top-left patch.

Similarly, for the operator that does not split (here the logical Z), we absorb the product of the split stabilizers into the newly defined operator. In this case, \(Z_\mathrm{control} = Z_\mathrm{aux} = Z_\mathrm{control\_new}\).
In Loom, the product of the split stabilizers is absorbed by the bottom-right patch.

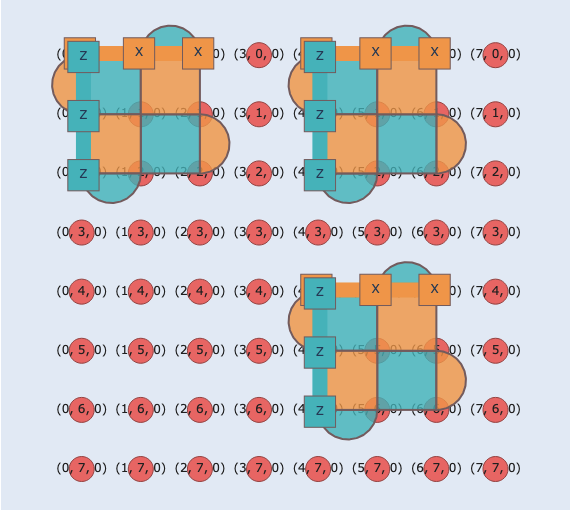
Step 3: Merge auxiliary and target blocks

We now merge aux and target into merged_target.
This operation joins two X-type boundaries, effectively performing a logical XX measurement.

The state of the merged block depends on the measurement outcome; we will correct for this in the next step.
At this point, we are also free to choose the logical operator for the merged qubit from among the unmerged logical operators of the original blocks (or a combination of them).
Loom follows the convention of selecting the logical operator of the top-left block.
In this example, merged_target inherits the X logical operator of the aux qubit.
It is important to keep track of this, as we will apply the corresponding correction in the next step.

We can now perform d rounds of syndrome extraction. Because the Merge operation already includes one round of stabilizer measurements, we only need to run d - 1 additional rounds on the merged target block.

Since control_new is idle during Merge, we can safely schedule its first error-correction round in parallel with the merge operation.

Step 4: Apply ConditionalLogicalZ

The AuxCNOT operation applies all necessary corrections automatically, keeping track of how the blocks are grown or shrunk, as well as their orientation.
In this example, we will explicitly illustrate each correction performed by AuxCNOT.

First, we correct based on the outcome of the Merge, i.e., the joint logical XX measurement on aux and target.

Loom supports conditional logical operations by allowing you to specify the conditions under which they apply.
Here, we use ConditionalLogicalZ, conditioned on the LogicalMeasurement of XX between aux and target, and apply this correction to the control_new block.

If the control block had been grown vertically, the joined boundaries would be Z-type, and the correction would instead be conditioned on a logical ZZ outcome.

Next, we apply an identical correction on merged_target block, which related to the choice of logical operator during the Merge.
By convention, we only need this correction when the logical operator inherited by the merged_target patch differs from that of the original target patch. This depends on the direction in which the target block is shrunk, specifically when it is "TOP" or "RIGHT".

If we had chosen the control and target roles differently, the merged target block would have inherited the logical operator from the original target block, and this correction would not be required.

Step 5: Shrink target

We then shrink the target block back to its original size.
The shrink direction is perpendicular to the original grow direction, and we shrink from the top of the qubit by d + 1 units.

Finally we can construct the Eka object and get the interpreted final circuit.

from loom.eka import Eka
from loom.interpreter import interpret_eka

eka_result = Eka(lattice, blocks=blocks, operations=auxcnot_operations)
interpreted = interpret_eka(eka_result, debug_mode=False)

We can visualize the plots shown in this tutorial as:

import loom.visualizer as vis

show_data_qubits = [True if q[2] == 0 else False for q in lattice.all_qubits()]

titles = ("Initialize", "Grow", "Split", "Merge", "Shrink")

for step, title in zip(range(5), titles):
    plot = vis.StabilizerPlot(lattice)
    plot.add_dqubit_traces(show_data_qubits)
    plot.plot_blocks(interpreted.block_history[step])
    plot._fig.update_layout(title=title, showlegend=False)
    plot._fig.update_layout(
        title = title,
        title_font=dict(size=22),
        margin=dict(t=60, l=30, b=30),
        width=680
    )
    plot.show()

---

Validate the result in Stim

We will now use Stim to check whether the created operation behaves as expected.
To do this, we generate a Bell pair and measure the logical qubits in the X or Z basis.
If the operation works correctly, the results should be random but always correlated.

We will: 1. Initialize the blocks in the \(|+\rangle\) and \(|0\rangle\) states
2. Run the AuxCNOT operations
3. Measure the logical qubits in the X or Z basis

import numpy as np
from loom.interpreter import interpret_eka
from loom.executor import EkaCircuitToStimConverter
import stim

converter = EkaCircuitToStimConverter()

for op in "X", "Z":
    operations = (
        ( # Reset
            ResetAllDataQubits("control", state="+"),
            ResetAllDataQubits("target", state="0"),
        ),
        ( # Measure syndromes 
            MeasureBlockSyndromes("control", n_cycles=d),
            MeasureBlockSyndromes("target", n_cycles=d),
        ),
        # AuxCNOT
        *auxcnot_operations, 
        ( # Measure syndromes 
            MeasureBlockSyndromes("control_new", n_cycles=d),
            MeasureBlockSyndromes("merged_target", n_cycles=d),
        ),
        ( # Measure logicals
            (
                MeasureLogicalX("control_new"),
                MeasureLogicalX("merged_target"),
            ) 
            if op == "X"
            else (
                MeasureLogicalZ("control_new"),
                MeasureLogicalZ("merged_target"),
            )
        )
    )

    # Convert to Stim circuit
    eka = Eka(lattice, blocks=blocks, operations=operations)
    interpreted = interpret_eka(eka, debug_mode=False)
    stim_circuit = converter.convert(interpreted)

    # Run simulation
    simulator = stim.TableauSimulator()
    simulator.do_circuit(stim_circuit)

    # Get observables
    # the last two measurement instructions in the circuit
    for meas_id, q_label in zip((2, 1), ("control", "target")):
        obs_instr = stim_circuit[-meas_id]
        meas_indices = [rec.value for rec in obs_instr.targets_copy()]
        meas_values = [
            simulator.current_measurement_record()[rec] for rec in meas_indices
        ]
        logical = np.bitwise_xor.reduce(meas_values)
        print(f"Logical {op} measurement on {q_label}:", int(logical))

You can run the cell above several times to obtain different shots from the simulator.
Recall that we initialized two qubits in the \(|+\rangle\) and \(|0\rangle\) states, respectively, and then applied a CNOT to create a Bell state, characterized by the stabilizer generators {+XX, +ZZ}.
We then measured both qubits either in the X basis or in the Z basis.
In both cases, the measurement outcomes should appear random, yet always correlated.

---

Summary

In this tutorial, we learned:

• How the AuxCNOT operation is composed of fundamental lattice-surgery primitives
• Use Grow, Split, Merge, and Shrinkto manipulate logical surface-code blocks
• Apply conditional logical operations based on measurement outcomes
• Interpret and visualize the evolution of logical blocks throughout the process
• Examine the result using Stim's TableauSimulator